Syllabus: PC_BK_04

Integration

The following description of integration and differentiation is from the website Math is Fun! 🙂 This is most likely all you will need to know about the subject for the FRCA. A one liner explanation for what it is – it is a mathematical method of determining the area under a curve. Don’t worry about the maths, it is very unlikely that you’ll be asked to do integration or differentiation during the exam. If they do, here’s a quick aide memoire:

If asked to integrate ∫3x² + 2x dx

The answer is x³ + x² + C.

More explanation on integration

Integration is a way of adding slices to find the whole.

What is the area under y = f(x) ? 

Slices

We could calculate the function at a few points and add up slices of width Δx like this (but the answer won’t be very accurate):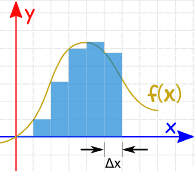
We can make Δx a lot smaller and  add up many small slices (answer is getting better):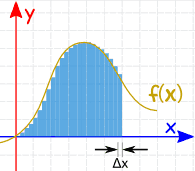
And as the slices approach zero in width, the answer approaches the true answer.We now write  dx to mean the Δx slices are approaching zero in width.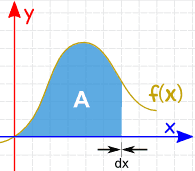

The symbol for “Integral” is a stylish “S” (for “Sum”, the idea of summing slices):

After the Integral Symbol we put the function we want to find the integral of (called the Integrand),

and then finish with dx to mean the slices go in the x direction (and approach zero in width).

And here is how we write the answer:

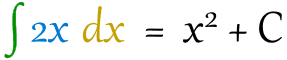
We wrote the answer as x² but why + C ? 

It is the “Constant of Integration”. It is there because of  all the functions whose derivative is 2x:

The derivative of x²+4 is 2x, and the derivative of x²+99 is also 2x, and so on! Because the derivative of a constant is zero. 

So when we reverse the operation (to find the integral) we only know 2x, but there could have been a constant of any value. 

So we wrap up the idea by just writing + C at the end.

Application of integration in anaesthetics: Calculation of volumes from a graph of gas flow against time (eg. patient blowing through a pneumotachograph), and cardiac output monitoring from the oesophageal doppler.

Differentiation

Differentiation is used in maths for calculating rates of change. 

For example in mechanics, the rate of change of displacement (with respect to time) is the velocity. The rate of change of velocity (with respect to time) is the acceleration.

If asked to differentiate the following:

y= 2x³ + 3x² + 5x + 4

The answer is f(x) = 3x² + 2x + 5.

More explanation on differentiation

The rate of change of a function f(x) with respect to x can be found by finding the derived function f′(x).

The derived function f′(x) = Slope = Gradient = Change in Y divided by Change in X = Δy divided by Δx

We write dx instead of  “Δx heads towards 0″.

And “the derivative of” is commonly written  :

x² = 2x
“The derivative of x² equals 2x“
or simply “d dx of x² equals 2x“

What does x² = 2x mean?

It means that, for the function x², the gradient, differential or “rate of change” at any point is 2x.

So when x=2 the slope is 2x = 4, as shown here:

Or when x=5 the slope is 2x = 10, and so on.

f’(x) is also used for “the derivative of”:

f’(x) = 2x
“The derivative of f(x) equals 2x”
or simply “f-dash of x equals 2x”